Telegram has a large and devoted user base. Despite WhatsApp being the most well-known messaging service, Telegram offers a more extensive range of features and greater security. The popular dark theme feature was made available to Telegram users long before it was introduced in WhatsApp’s beta version. When it comes to user security, Telegram is considered safe and provides various options for users to protect themselves online while using the application. However, some users have reported issues while logging in. If you are experiencing such problems, then you have come to the right place.
Also Read
Fix: Telegram Desktop Notification Not Working
5 Easy Ways to Turn Off Phone without Power Button (Android)
Fix: Telegram Not Downloading When Screen is off or in Background
Fix: Telegram Calls Not Ringing on Android and iPhone
Telegram Calls Recorder for Android and iPhone
Telegram Showing Line Busy, What Does It Mean?
Fix: Telegram Video Call Not Working on Android, iPhone and Desktop
10 Best Ways to Increase Telegram Download Speed on PC, Android, iPhone
Where to Find Telegram Downloaded Files on Android, iPhone, and PC
Free Proxy Address for Telegram | List of All Proxy Server 2023
As in this post, we will guide you on how to fix common Telegram login problems and their dedicated solutions to them. Though Telegram is a wonderful messaging app that I personally prefer over WhatsApp, certain login issues are very common with any messaging app and in this post, we will guide you on how to fix those. So, without any further ado, let us get straight into the article itself:
Also Read: How to fix This Telegram Channel Cannot be Displayed Error?
Page Contents
Common Telegram Login Problems and Solutions
You can troubleshoot several log-in related issues on the Telegram by following the below-mentioned guide:
Did not receive a login code
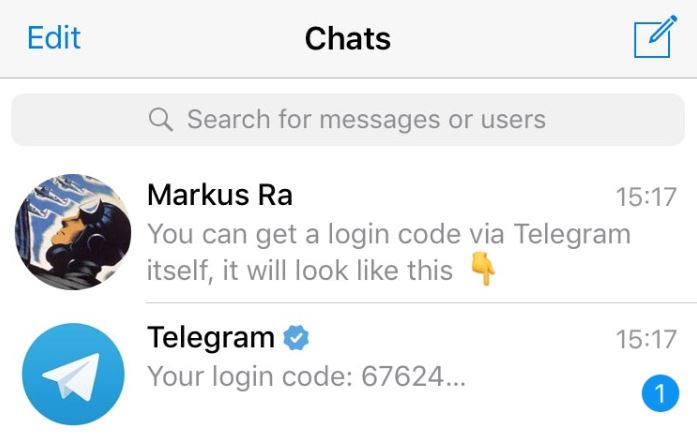
There are certain issues where users have reported not receiving the login code to enter and log in to use the Telegram application. A simple workaround is that if you are logged in to another device then, Telegram sends you the code via Telegram and not via SMS. This negates the possibility of your poor network connection and issues of having different mobile numbers. You just need to check in to the device where you are logged in.
In case you have not received the code, you can use the option “Haven’t received the code?” and request the code via SMS. You can even request Telegram to let you know your code via phone call as well.
Too many attempts
The Too many attempts error shows up when you have attempted to log in with a wrong code multiple times recently. In this case, you should wait for 24 hours before you can log in again. Moreover, if you are also wanting to know what is the actual time left before you can go ahead and log in then, you can visit web.telegram.org and attempt to sign in, and then click on the “show technical details” then it will show you the timer with the exact amount of time that you need to wait before you can log in.
Limit exceeded or Internal server error
If you have deleted your accounts too many times then, you will be shown errors like limit exceeded or internal server error. You need to simply need to wait a couple of weeks before you can go ahead and try signing up.
Banned phone number or Your phone was banned
If while logging in, the Telegram shows you an error message of Banned phone number or your phone was banned then and you think that it has been accidentally done then, you can report this issue by sending a DM on Twitter with your phone number: @smstelegram.
So, there you have it from my side in this post. I hope you guys liked this post and were able to troubleshoot common problems related to the Telegram application. Let us know in the comments below if you liked this post and were able to fix the issues that you are facing. Until the next post…Cheers!

ugh! No matter what I’ve tried , Telegram never sends a code anymore. I waited several days again before trying….I’ve deleted app, then re downloaded. I’ve tried from my computer. Same thing….no code is ever sent. No code sent on my phone. I get no prompts or messages or even any choices to see what’s going on. I’ve never actually posted anything on Telegram but look at all the channels that i’m subscribed to. I have re-posted other telegrams… There is nothing that I would’ve done to get my number banned. I haven’t received that message either. There is just no code sent…….It stopped working about 2 weeks ago…no code sent. I’ve done all the steps you mention too. Still nothing.
Use Vpn
Solution:
I was having same issue when I tried to open my telegram app the only message was connecting and after waiting for hours it didn’t connect, then I uninstall the app and install it again but the problem persist, I log out and again for logging after entering the Mobile number it was just scrolling, then I use VPN and it worked so my advice to all those who are facing same issue use VPN, it will work
Dear sir/ madam my login problem please reset in my account
Same problem bro
I signed up today, signed in etc. later when I wanted to sign in it insists on sending another code, so I get that code, again later to sign in, another code. Eventually it said to many tries and shut me out for 24 hours. I totally despise this app for not being able to simply sign in to be able to communicate. Now I’m locked out from my family. So much for European tech. Rubbish! It’s gone now.
No help at all unfortunately I am still locked out! I accidently logged out 2 days ago and Telegram log in will not send code and has locked me out again! Please any other suggestions? I love Telegram but they have no tech support. I even went the route of filling out their help form…several times now!
Use vpn
Using a VPN won’t fix this problem, no matter how many times you type it in the comments.
Also, if I can’t log into Telegram how is it possible to get into the chat??? please advise if you know, thank you!
Login issue didn’t get the code
Same issue. Didnt get code. Always connecting issue
Why I cant log in to my Telegram?
Log in issue didn’t get the code.
“Did not receive a login code” to mobile advice does not work when the Telegram login was on a computer where the hard disk has failed. Any solution? Clicking ‘Send code via SMS’ says ‘Please enter the code that was sent to you via Telegram or log in via QR code.’ That’s useless, i have a 3G phone (for good reason) that does not qr.
Use vpn
My tegram didnt work
Sir to many attempt plz help
Logging issues Otp not received
My mobile no-0701966945
I’m a srilanken
In lest 10 days before icant to log my telegram account
I want to loggin now
Plz give me access
I cant find the telegram code to login please help
Iam not login my account
you need to have telegram on another device i.e. a laptop or phone and have telegram open, use a different phone number perhaps a family member. Then you can see the code.
New login. Dear Khursed, we detected a login into your account from a new device on 08/06/2022 at 04:14:54 UTC.
Device: Telegram Android, 8.7.4, Samsung Galaxy M32, Android, 11 R? (30)
Location: Delhi, India (IP = 157.37.176.180)
If this wasn’t you, you can terminate that session in Settings > Devices (or Privacy & Security > Active Sessions).
If you think that somebody logged in to your account against your will, you can enable Two-Step Verification in Privacy and Security settings.
My telegram is showing “Connecting ” from past two days. Though it did not show any message or any errors. I deleted the app without deactivating/deleting my account. It’s not even moving ahead of where we give our contacts.
Same issue. Did you find the solution?
This information is outdated. The option now is to receive a code on the “other device” or to open the app on your phone and scan a QR code. I need information on how to log in on a laptop with no phone app. This problem is new as of mid May 2021.
My telegram bolemy
why did haven’t password
Iam not login my account and my account has been deleted
Telegram used to require emails to log in. Now it only accepts phone numbers. 2 questions:
1. I have an account that I can no longer access because it’s connected to my email address. I have contacts in that account.
2. What if you don’t have a working phone number at the time?
telegram too many attempts please try again later
My account block help me but Don’t forget pinned masage problems help sir
Too many attempts
I have tried to use Telegram so many times s and it will not send me the code. I have a high-speed internet connection and I have no issues getting text so it’s frustrating when all my friends are using Telegram but I can’t.
Use vpn
Same issues here the worst thing is that I have to join stunds groups on these app but it keeps on requesting me a password that I don’t have cause I have never used this app before
Same!
Haven’t received code please send via sms,+27685401425
Why do you make it so difficult to sign up?
No other devices, no code, no message, no Telegram, no play time….
Please how can I know when to try later, I was trying to login but I was told to try again later
I mean what exact time should I check it back. Have tried checking web.telegram.org but I didn’t see the remaining time
I am logged in TG on the phone and am trying to log in into an app on the desktop. But the login by QR code is not working, neither is the login by a sent code, because that code never arrives.
Same problem. just wondering if you ever got in, and how.
Thanks, Allen
My laptop with telegram installed crashed. After reinstallation of the laptop i downloaded Telegram again. I tried to login with my phone number and waited for a code…NOTHING!! I have a gsm, no smartphone.
I have used telegram for a few months. When I want to leave and close the site all I do is close the screen and turn off the computer. I recently tried to delete the annoying ping that I receive when other members of the group are chatting. I accidently pushed the Log Out link and hey – presto cannot get back in. Same problem as other users trying to access a code.
I have got a code from you but when I try to get into telegram it just flashes on then off no time to put any thing in at all. I am still getting message banners but if I click on them nothing happens
Hi, i’ve Telegram Desktop SW installed and wanted to login by my mobil phone number. It’s not a smartphone. The requested to type in a code, but i didn’t get any code, for example, as SMS or so whether to my mobil phone nor to my email account.
What can i do to access Telegram?
Thanx in advance!
Roland
Tried several times,won t send code to sign in
I am having exactly the same problem and that for the last 2 months can not access Telegram anymore … Using my computer desk to access telegram when I put my mobile number with the area code etc it tells me the code has been sent on my mobile but never have received the code … I even had notified Telegram twice of the recurrent problem never received a reply !!!! Can you please let me know how can re access my telegram ..Very very frustrating ! And I see I am not the only one ..Thank you
I got a new cellphone. Now I can’t get into my telegram account. I have requested an SMS code so many time and never received a code. That I am now apparently locked out.
Iam not login my account and my account has been deleted
I can’t log into Telegram. The SMS code has not been received by my phone (many attempts). This app worked fine in previous phone. Got a new replacement phone (same exact kind) and now I can no longer access the app. I think I am giving up on Telegram – support is nonexistent.
Hello,im having a problem logging in to telegram,i have been logged out,its showing me no options of receiving code by SMS or phone,i have been using same device and I need to get in, my number +27685401425,please help
Question. When I add members to a telegram group, the ID banned
Why can’t I log in to my telegram it says pls check internet connection, my internet has great signal and connection why?
Utterly useless.
Been using Telegram for PC for ages without a problem, then a few days back it just wouldn’t open.
I discover now that desktop users no longer receive a code via sms, instead I have to log in via some “QR code” on another device.
Well, that’s useless to me. I don’t have a phone or any other “device”, just my pc.
Goodbye Telegram, such a shame your customer support was so poor.
log in after 2weeks just for repeated deletion and sign in attempts? poor app.. poor tech support..
Such problems wouldnt exist if only login codes and set immediately after its users attempt to login..Might as well delete it and never download it again..PPPPOOOOOORRRRR AAAAPPPPP..
How about you tell us how to fix it without trying to sell WhatsApp which is a garbage app.
Why are they saying they send code to my other device? My phone has been hacked in the past. Should I be concerned
I haven’t received activation code plz help
Telegram is best
I have been trying to help several friends login to Telegram. 2 are new accounts, and 1 is a guy who’s computer crashed and we had to reload the OS from scratch. Nobody can get the SMS code for verification.
So… I tried using a VPN – that didn’t work either. I think it may be possible that the CIA or some .gov agency is DDOSing the Telegram website to prevent people from using Telegram because the Govt doesn’t want any of us to access the truth of what is happening with Covid and Ukraine.
The Govt doesn’t like Telegram and wants us to accept the MSM narrative.
Trying to login but was told to check my internet connection and try again meanwhile I don’t have internet problem
Didn’t get my login code
Mine is also same
I suspect, hackers, hacked my mob numbers
+91 9444403510 &
+91 7094800724
If I put some other mob number my Mrs number, in my instrument, it, acknowledges, and request to log in with her Gmail, I’d, if I, log in, it sends log in or call to my Mrs number, I did not log in because it is my Mrs number, regards
I have multiple account on my telegram application both in my android phone and in my PC buy the problem is :
I can’t connect to one of my account neither on PC nor in my phone by proxy but other accounts in the same app can be run smoothly
it means that I don’t have a domestic problem and the issue is from Telegram maybe
New login. Dear Khursed, we detected a login into your account from a new device on 08/06/2022 at 04:14:54 UTC.
Device: Telegram Android, 8.7.4, Samsung Galaxy M32, Android, 11 R? (30)
Location: Delhi, India (IP = 157.37.176.180)
If this wasn’t you, you can terminate that session in Settings > Devices (or Privacy & Security > Active Sessions).
If you think that somebody logged in to your account against your will, you can enable Two-Step Verification in Privacy and Security settings.
Dear sir/ madam my login problem please reset in my account
I can’t get the code to register my number
A very simple solution worked for me.
disable any other phone app or sms app you are using like true caller or similar kind,
Revert your phone app and message app to the default stock app.
Now try it
Hope it works
Unfortunately, my telegram is Logout and if i open & start my telegram and enter the login code, it says enable two step verification and it is protected additional password, so please help me
Hi,my account also can’t login.
Last 2 day change my phone and login again this issue.please reset my account and help
+9595414805
Myanmar
Hi,my account also can’t login.
Last 2 day change my phone and login again this issue.please reset my account and help Me
+9595414805
Last 2 day change my phone and login again this issue.please reset my account and help Me
+9595414805
Haven’t received any code two weeks now please sent +265881102476
Please we cannot access our accounts
You are becoming inefficient
I am not able to login to my telegram account from yesterday onwards as it shows an invalid email address error or phone code expired
Telegram has betrayed its faithful Users… with all of this bullshit….strange how my computer blows up then telegram pulls this shit and will not send me a Flulck code to mt fulking phone… Thanks for nbothing telegram!!!!!!
Telegram has betrayed its faithful Users… with all of this bullshit….strange how my computer blows up then telegram pulls this shit and will not send me a Flulck code to mt fulking phone… Thanks for nothing telegram!!!!!!
I am not too pleased myself. I changed phones. I have the same phone number as I had when I first got my telegram account, but now with my new phone I am unable to login to telegram. Telegram, how about making it easier to login? And by the way, how about also ditching the qr codes?? In my eyes, those qr codes are NOT secure or safe!! A good old fashioned strong password is much better! And since I use a password generator, mine are unique each time I generate one for a new service or site and difficult to crack because they are 100 percent random.
i think telegram became too much of a game changer and got destroyed…
i have no way of accessing also
Don’t get my Telegram code
00959650525561
00959250760943
Plz , help me
I’ve logged out from my telegram account two days ago on my computer, was using telegram desktop. When trying to log in again, it proposed qrcode, I clicked on logging by phone but it was impossible to get SMS to my simple phone, telegram is keeping sending code to my telegram which is not logged in since I logged out. When I ask SMS it shows an error window and no other possibility. Can’t use my telegram anymore, because the same problem applies even if I disinstall telegram and then install it again, on windows10 laptop.